periods. The actual formula for the speed of the wave
train is
C=1.515T
where C is the speed of the wave train and T is the
wave period in the wave train.
All of the different wave trains (series of waves all
having the same period and direction of movement) in
the fetch can be compared to a group of long distance
runners at a track and field meet. At first all of the
runners start out at the starting line at the same time. As
they continue on, however, the faster runners move
ahead and the slower runners begin to fall behind. Thus
the field of runners begins to string out along the
direction of travel. The wave trains leaving a fetch do
the same thing. The stringing out of the various groups
of waves is called dispersion.
In a swell forecast problem it is necessary to
determine what wave trains have already passed the
forecast point and which have not yet arrived. After this
has been determined, the wave trains that are left are the
ones that are at the forecast point at the time of
observation.
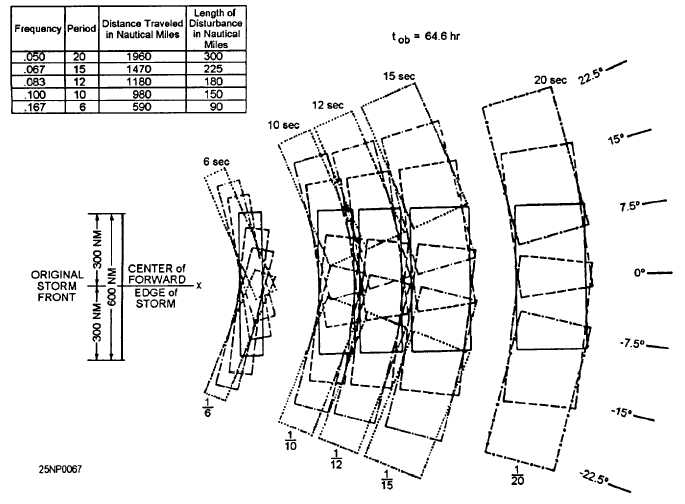
Angular Spreading
As the wave trains leave the fetch, they may leave
at an angle to the main direction of the wind in the fetch.
Thus, swell waves may arrive at a forecast point though
it may lie to one side of the mainline of direction of the
wind. This process of angular spreading is depicted in
figure 6-6.
The problem in swell forecasting is to determine
how much of the swell will reach the forecast point after
the waves have spread out at angles. This is
accomplished by measuring the angles from the leeward
edge of the fetch to the forecast point. These angles
must be measured as accurately as possible, figure 6-7,
and are determined by the following five rules:
1. Draw the rectangular fetch.
Figure 6-6.-Angu1ar spreading.
6-10