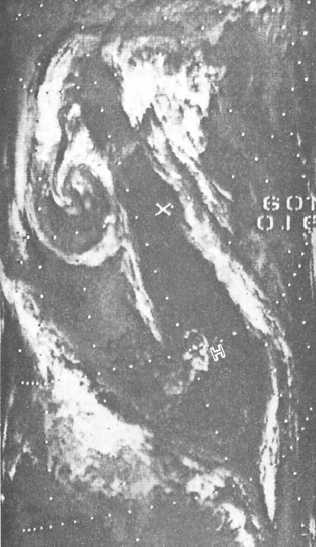
Figure 3-15.-Infrared, local midnight, third night.
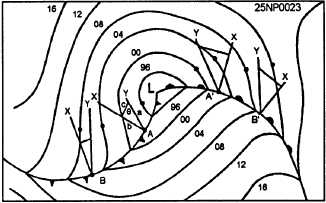
vector, letting it intersect the “y” vector. This is line c in
figure 3-16.
5. The angle formed at the intersection of the “y”
vector and the perpendicular originating from the “x”
vector is labeled
q
(theta). Measure angle
q
to the
nearest degree with a protractor, and determine the
value of its sine by using trigonometric tables or a slide
rule.
6. Let side a of the right triangle formed in step 4
represent the value of the geostrophic wind obtained in
step 1, and call it “Cgs.” Solve the triangle for side b by
multiplying the sine of
q
by the value of Cgs. The
resulting value of b is the component of the wind
normal to the front, giving it its forward motion. The
formula is
b= Cgs x sin
q
Figure 3-16.-Geostrophic wind method.
In the sample problem, if the Cgs was determined to
be 25 knots and angle
q
to be 40°, b is 19.1 knots, since
the sine of angle
q
is 0.643.
As you can see, the components normal to the front
should be equal on both sides of the front, and that in
reality, it would matter very little where the component
is computed in advance of or to the rear of the front. In
cold fronts the reason that the component to the rear is
chosen is that this flow, as well as this air mass, is the
flow supplying the push for the forward motion. In the
case of a warm front, the receding cold air mass under
the warm front determines the forward motion, because
the warm air mass is merely replacing the retreating
cold air, not displacing it.
OTHER CONSIDERATIONS.— The foregoing
discussion neglected to discuss the effects of cyclonic
and anticyclonic curvature on the isobars, and the effect
of vertical motion along the frontal surfaces. The
upslope motion along the frontal surfaces reduces the
effective component normal to the front. Furthermore,
the cyclonic curvature in the isobars indicates
convergence in the horizontal and divergence in the
vertical, further reducing the effective component
normal to the front. For these reasons, the component
normal to the front is reduced at the surface only by the
following amounts for the different types of fronts and
isobaric curvature:
Slow moving cold front,
anticyclonic curvature . . . . . . . . 0%
Fast moving cold front,
cyclonic curvature . . . . . . . . 10-20%
Warm front . . . . . . .
. . . . . .20-40%
Warm occluded fronts . . . . . . . . 20-40%
Cold occluded fronts . . . . . . . . . 10-30%
3-19