originally stable may become unstable due to moisture distribution if the entire layer is lifted. Convective  stability  is  the  condition  that  occurs when  the  equilibrium  of  a  layer  of  air,  because  of  the temperature   and   humidity   distribution,   is   such   that when the entire layer is lifted, its stability is increased (becomes more stable). Convective instability is the condition of equilibrium   of   a   layer   of   air   occurring   when   the temperature and humidity distribution is such that when the entire layer of air is lifted, its instability is increased (becomes more unstable). CONVECTIVE STABILITY.—Consider a layer of air whose humidity distribution is dry at the bottom and moist at the top. If the layer of air is lifted, the top and  the  bottom  cool  at  the  same  rate  until  the  top reaches saturation. Thereafter, the top cools at a slower rate of speed than the bottom. The top cools saturation adiabatically   (.55°C/100   meters),   while   the   bottom continues  to  cool  dry  adiabatically  (1°C/100  meters). The  lapse  rate  of  the  layer  then  decreases;  hence,  the stability increases. The layer must be initially unstable and may become stable when lifting takes place. CONVECTIVE    INSTABILITY.—Consider    a layer of air in which the air at the bottom is moist and the air at the top of the layer is dry. If this layer of air is lifted,  the  bottom  and  the  top  cool  dry  adiabatically until the lower portion is saturated. The lower part then cools saturation adiabatically while the top of the layer is  still  cooling  dry  adiabatically.  The  lapse  rate  then begins to increase and instability increases. To determine the convective stability or instability of a layer of air, you should first know why you expect the lifting of a whole layer. The obvious answer is an orographic barrier or a frontal surface. Next, determine how much lifting is to be expected and at what level it commences. Lifting of a layer of air close to the surface of the Earth is not necessary. 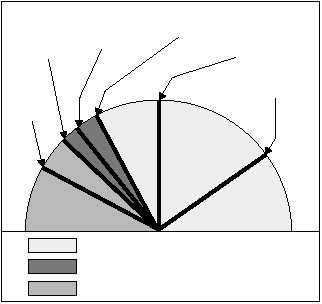The amount of lifting, of course,  depends  on  the  situation  at  hand.  Figure  2-15 illustrates  the  varying  degrees  of  air  stability  that  are directly  related  to  the  rate  at  which  the  temperature changes with height. Determining Bases of Convective Type Clouds You have seen from our foregoing discussion that moisture  is  important  in  determining  certain  stability conditions  in  the  atmosphere.  You  know,  too,  that  the difference between the temperature and the dew point is an  indication  of  the  relative  humidity.  When  the  dew point  and  the  temperature  are  the  same,  the  air  is saturated and some form of condensation cloud may be expected. This lends itself to a means of estimating the height of the base of clouds formed by surface heating when the surface temperature and dew point are known. You know that the dew point decreases in temperature at the rate of 1°F per 1,000 feet during a lifting process. The    ascending    parcel    in    the    convective    current experiences a decrease in temperature of about 5 1/2°F per 1,000 feet. Thus the dew point and the temperature approach each other at the rate of 4 1/2°F per 1,000 feet. As an example, consider the surface temperature to be 80°F  and  the  surface  dew  point  62°F,  a  difference  of 18°F. This difference, divided by the approximate rate the temperature approaches the dew point (4 1/2°F per 1,000 ft) indicates the approximate height of the base of the clouds caused by this lifting process (18 ÷ 4 1/2) × 2-21 AG5f0215 STABLE CONDITIONALLY UNSTABLE UNSTABLE NORMAL LAPSE RATE MOIST ADIABATIC ADIABATIC ISOTHERMAL SUPER ADIABATIC INVERSION Figure 2-15.—Degrees of stability in relation to temperature changes with height.