If we substitute the known information in figure
2-2 we have the following:
C2 = Unknown resultant force
a2 = 5 lb or the known force on one side of our
right triangle, side BX (same as side AC)
b2 = 10 lb or the known force on the other side
of our right triangle, side AB
Setting up the equation we have:
C2 = a2 +
C2 = 52 + 102
C2 = 25 + 100
C2 = 125
C = 125
C = 11.18034
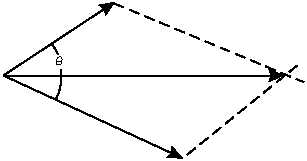
To find the resultant of two forces that are not at
right angles, the following graphic method may be
used. (See fig. 2-3).
Let AB and AC represent the two forces drawn
accurately to scale. From point C draw a line parallel to
AB and from point B draw a line parallel to AC. The
lines intersect at point X. The force AX is the resultant
of the two forces AC and AB. Note that the two dashed
lines and the two given forces make a parallelogram
ACXB. Arriving at the resultant in this manner is called
the parallelogram method. The resultant force and
direction of the resultant is found by measuring the
length of line AX and determining the direction of line
AX from the figure drawn to scale. This method applies
to any two forces acting on a point whether they act at
right angles or not. Note that the parallelogram
becomes a rectangle for forces acting at right angles.
With a slight modification, the parallelogram method of
addition applies also to the reverse operation of
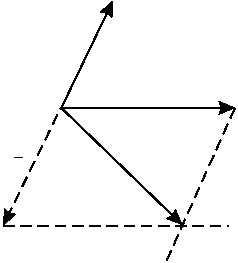
subtraction. Consider the problem of subtracting force
AC from AB. (See fig. 2-4.)
First, force AC is reversed in direction giving -AC
(dashed line). Then, forces -AC and AB are added by
the parallelogram method, giving the resulting AX,
which in this case is the difference between forces AB
and AC. A simple check to verify the results consists of
adding AX to AC; the sum or resultant should be
identical with AB.
Application of Vectors and Resultant Forces
The methods presented for computing vectors and
resultant forces are the simplest and quickest methods
for the Aerographer’s Mate. The primary purposes of
using vectors and resultant forces are for computing
radiological fallout patterns and drift calculations for
search and rescue operations.
REVIEW QUESTIONS
Q2-1.
What is the definition of speed?
Q2-2.
What is the correct formula for work?
Q2-3.
What are the two types forces that AGs deal
with?
MATTER
LEARNING OBJECTIVE: Recognize how
pressure, temperature, and density affect the
atmosphere. Describe how the gas laws are
applied in meteorology.
Matter is around us in some form everywhere in our
daily lives—the food we eat, the water we drink, and
the air we breathe. The weather around us, such as hail,
rain, invisible water vapor (humidity), etc., are all
2-4
AG5f0203
C
A
(R) RESULTANT
B
X
Figure 2-3.—Graphic method of the composition of forces.
C
B
C
X
A
AG5f0204
Figure 2-4.—Parallelogram method of subtracting forces.