put on an object directly through physical contact. An
example of contact force is the force your hand exerts
when you push your coffee cup across a table. Contact
force may act in several different directions at once as
well. For example, the force exerted by water in a can is
equally exerted on the sides and the bottom of the can.
In addition, an upward force is transmitted to an object
on the surface of the water. Forces that act through
empty space without contact are known as action at a
distance force. An example of this force is gravity.
Vectors
Problems often arise that make it necessary to deal
with one or more forces acting on a body. To solve
problems involving forces, a means of representing
forces must be found. True wind speed at sea involves
two different forces and is obtained through the use of
the true wind computer. Ground speed and course of
aircraft are computed by adding the vector representing
aircraft heading and true air speed to the vector
representing
the
wind
direction
and
speed.
In
computation of the effective fallout wind and other
radiological fallout problems, the addition of forces is
used. From these examples, it is evident that the
addition
and
subtraction
of
forces
has
many
applications in meteorology.
A
force
is
completely
described
when
its
magnitude, direction, and point of application are
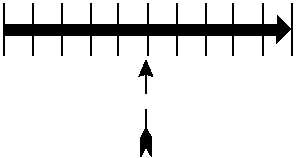
given. A vector is a line that represents both magnitude
and direction; therefore, it may be used to describe a
force. The length of the line represents the magnitude
of the force. The direction of the line represents the
direction in which the force is being applied. The
starting point of the line represents the point of
application of the force. (See fig. 2-1.) To represent a
force of 10 pounds or 10 knots of wind acting toward
due east on point A, draw a line 10 units long, starting at
point A and extending in a direction of 090°.
Composition of Forces
If two or more forces are acting simultaneously at a
point, the same effect can be produced by a single force
of the proper size and direction. This single force,
which is equivalent to the action of two or more forces,
is called the resultant. Putting component forces
together to find the resultant force is called composition
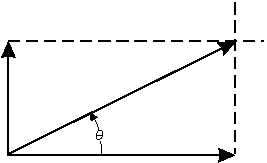
of forces. (See fig. 2-2.) The vectors representing the
forces must be added to find the resultant. Because a
vector represents both magnitude and direction, the
method for adding vectors differs from the procedure
used for scalar quantities (quantities having only
magnitude and no direction). To find the resultant force
when a force of 5 pounds and a force of 10 pounds are
applied at a right angle to point A, refer to figure 2-2.
The resultant force may be found as follows:
Represent the given forces by vectors AB and AC
drawn to a suitable scale. At points B and C draw
dashed lines perpendicular to AB and AC, respectively.
From point A, draw a line to the point of intersection X,
of the dashed lines. Vector AX represents the resultant
of
the
two
forces.
Thus,
when
two
mutually
perpendicular forces act on a point, the vector
representing the resultant force is the diagonal of a
rectangle. The length of AX, if measured on the same
scale as that for the two original forces, is the resultant
force; in this case approximately 11.2 pounds. The
angle gives the direction of the resultant force with
respect to the horizontal.
Mathematically,
the
resultant
force
of
perpendicular forces can be found by using the
Pythagorean theorem which deals with the solution of
right triangles. The formula is C2 = a2 + b2. This states
that the hypotenuse, side “C” (our unknown resultant
force) squared is equal to the sum of side “a” (one of our
known forces) squared and side “b” (another of our
known forces) squared.
2-3
N
A
10 LB
AG5f0201
Figure 2-1.—Example of a vector.
AG5f0202
C
X
5 LB
10 LB
B
A
Figure 2-2.—Composition of two right angle forces.