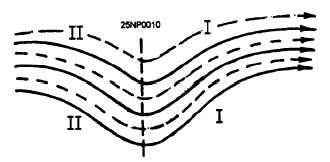
Place a small parcel at the trough and ridge lines and
observe the way the flow will spin the parcel, causing
vorticity. The diameter of the parcel will be rotated from
the solid line to the dotted position (due to the northerly
and southerly components of the flow on either side of
the trough and ridge lines).
Note that we have counterclockwise rotation at the
trough (positive vorticity), and at the ridge line we have
clockwise rotation (negative vorticity). At the point
where there is no curvature (inflection point), there is no
turning of the parcel, hence no vorticity. This is
demonstrated at point Pin figure 1-5.
Combined Effects
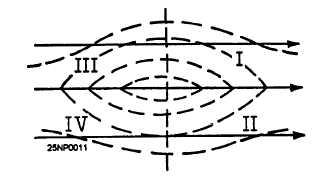
To find the relative vorticity of a given parcel, we
must consider both the shear and curvature effects. It is
quite possible to have two effects counteract each other;
that is, where shear indicates positive vorticity but
curvature indicates negative vorticity, or vice versa (fig.
1-6).
To find the net result of the two effects we would
measure the value of each and add them algebraically.
The measurement of vorticity will be discussed in the
next section.
It must be emphasized here that relative vorticity is
observed instantaneously. Relative vorticity in the
atmosphere is defined as the instantaneous rotation of
very small particles. The rotation results from wind
shear and curvature. We refer to this vorticity as being
relative, because all the motion illustrated was relative
to the surface of the Earth.
ABSOLUTE VORTICITY
When the relative vorticity of a parcel of air is
observed by a person completely removed from the
Earth, he or she observes an additional component of
vorticity created by the rotation of the Earth. Thus, this
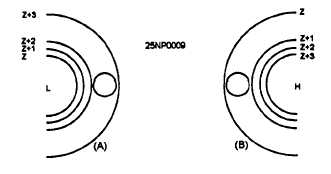
Figure 1-6-Illustration of shear effect opposing the curvature
effect in producing vorticity. (A) Negative shear and positive
curvature; (B) positive shear and negative curvature.
Figure 1-7.-Contour-isotach pattern for shear analysis.
person sees the total or absolute vorticity of the same
parcel of air.
The total vorticity, that is, relative vorticity plus that
due to the Earth’s rotation, is known as the absolute
vorticity. As was stated before, for practical use in
meteorology, only the vorticity about an axis
perpendicular to the surface of the Earth is considered.
In this case, the vorticity due to the Earth’s rotation
becomes equal to the Coriolis parameter. This is
expressed as 2oI sin Ø, where w is the angular velocity
of the Earth and Ø is the latitude. Therefore, the
absolute vorticity is equal to the Coriolis parameter plus
the relative vorticity. Writing this in equation form
gives: (Za = absolute vorticity)
Za=2cosin0+Zr
EVALUATION OF VORTICITY
In addition to locating the areas of convergence and
divergence, we must also consider the effects of
horizontal wind shear as it affects the relative vorticity,
and hence the movement of the long waves and
deepening or falling associated with this movement.
The two terms curvature and shear, which
determine the relative vorticity, may vary inversely to
each other. Therefore, it is necessary to evaluate both
of them. Figures 1-7 through 1-10 illustrate some of the
possible combinations of curvature and shear. Solid
Figure 1-8.-Contour-isotach pattern for shear analysis.
1-9